Stochastic resonance

In digging through old models and scripts, I came upon one to illustrate the concept of stochastic resonance. In short, when noise is added to periodic signals with local stability, it can cause them to jump between equilibria at about the dominant frequency:

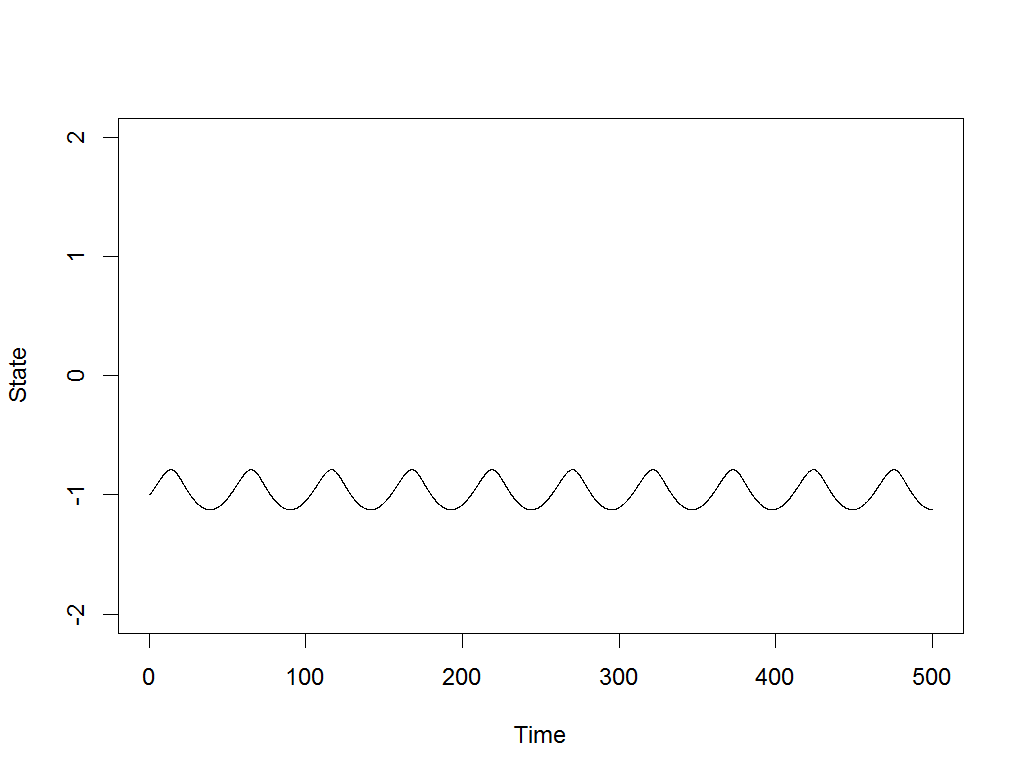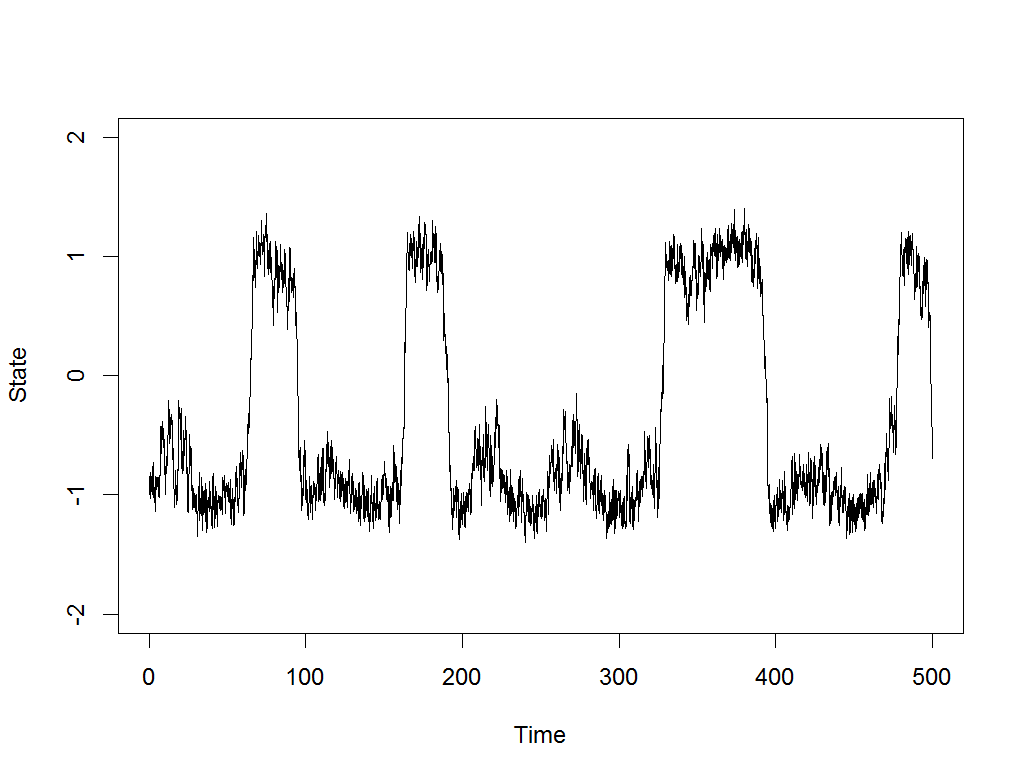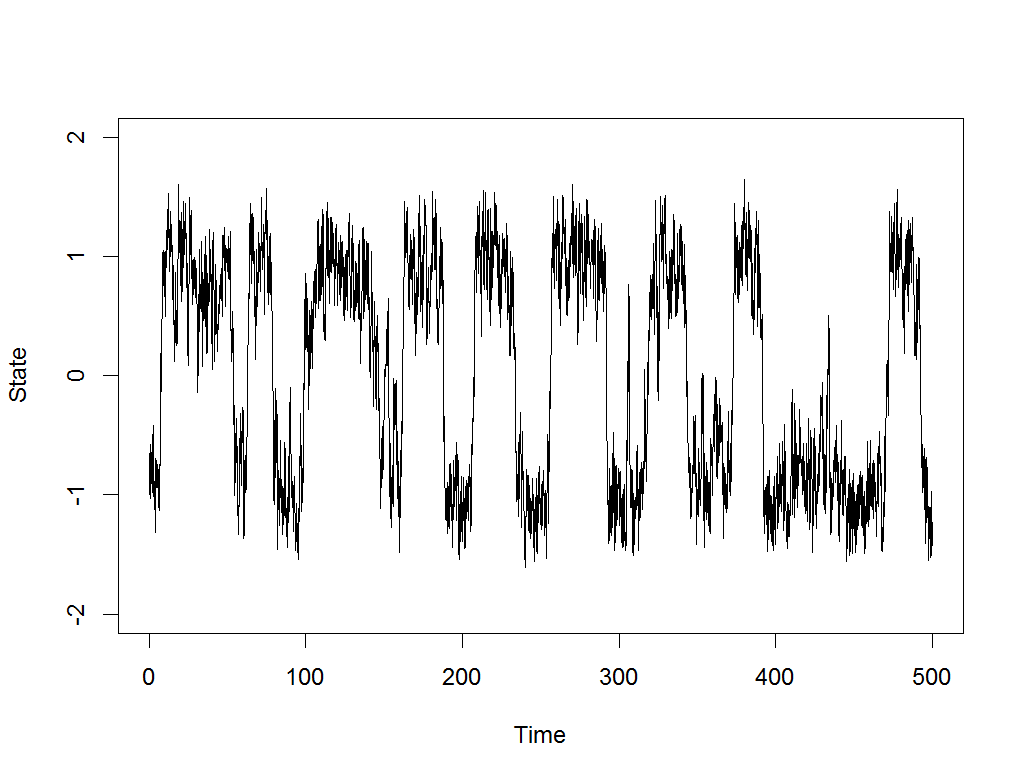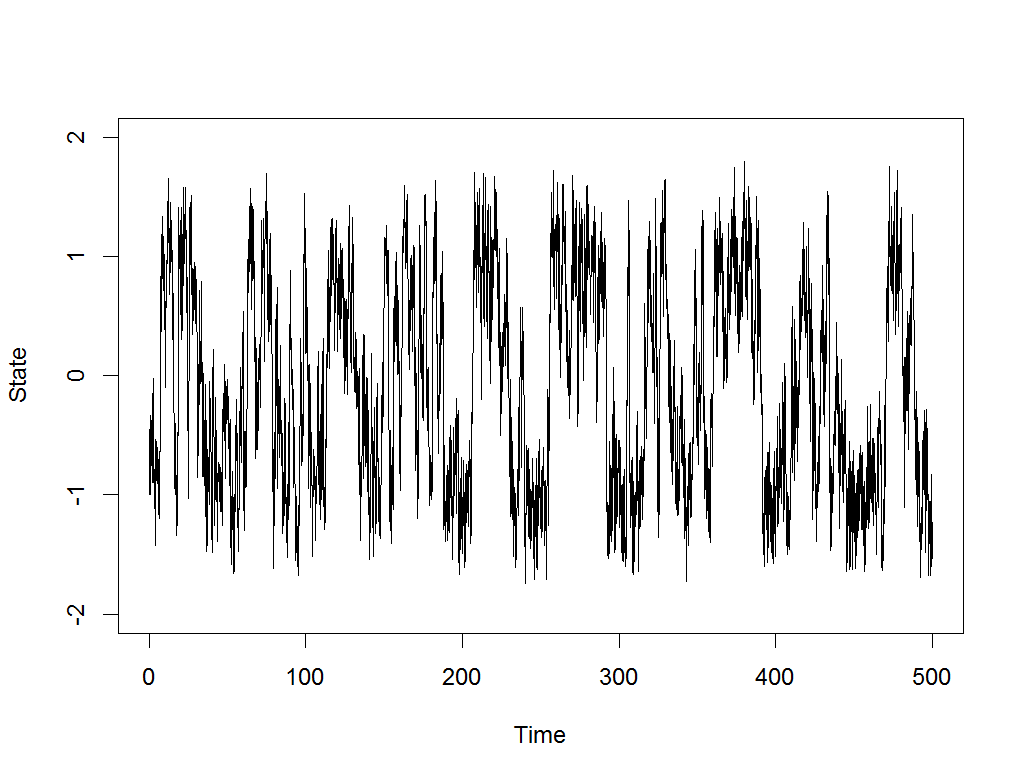
We are always looking for interesting statistical phenomena like this for models in computational psychiatry, where symptoms of mania or depression, for example, are often episodic and make large, spontaneous leaps after periods of relative stability.

The above example was produced by the following nonlinear equation with a sinusoidal force and noise term:

$$ \frac{dy(t)}{dt} = y(t)-y(t)^3 + .3\sin (.1225t) + \delta(t),\quad \delta(t) \sim N(0,1)$$

R code to generate the above animation:

library(deSolve)

dwp<-function(t,  y, parms){
  with(parms, {
    dy<- y - y^3  + .3*sin(.35^2 * t ) + rnorm(1, 0, sigma)
    return(list("dy"=dy))
  })
}

Time<-500
dt<-.1
sigs<-seq(0, 5, length.out=50)
for(i in 1:length(sigs) ){
  set.seed(123)
  sig<-sigs[i]
  x<-rk4(y=-1,t=seq(dt, Time, by=dt), dwp, parms=list("dt"=dt, "Time"=Time, "sigma"=sig))
  png(paste0("stochres/",i,".png"), width=1024, height=780, pointsize = 24)
  plot(x, type="l", ylim=c(-2,2), main="", xlab="Time", ylab="State")
  dev.off()
}