github repository for this project
Part 3 of my neural network project in R involves coding a recurrent version of the Helmholtz machine. A recurrent (i.e., autoregressive or time-lagged) version of the network follows naturally (kind of), and of course, Hinton already published the idea in 1995. I used his paper as a guide to be sure nothing was markedly different about the approach and coded it according to my previous strategy.
This graphic should help understand the difference in model structure, with the top two indicating the recognition (left) and generation (right) networks of a basic Helmholtz machine, simplified to one node per layer:
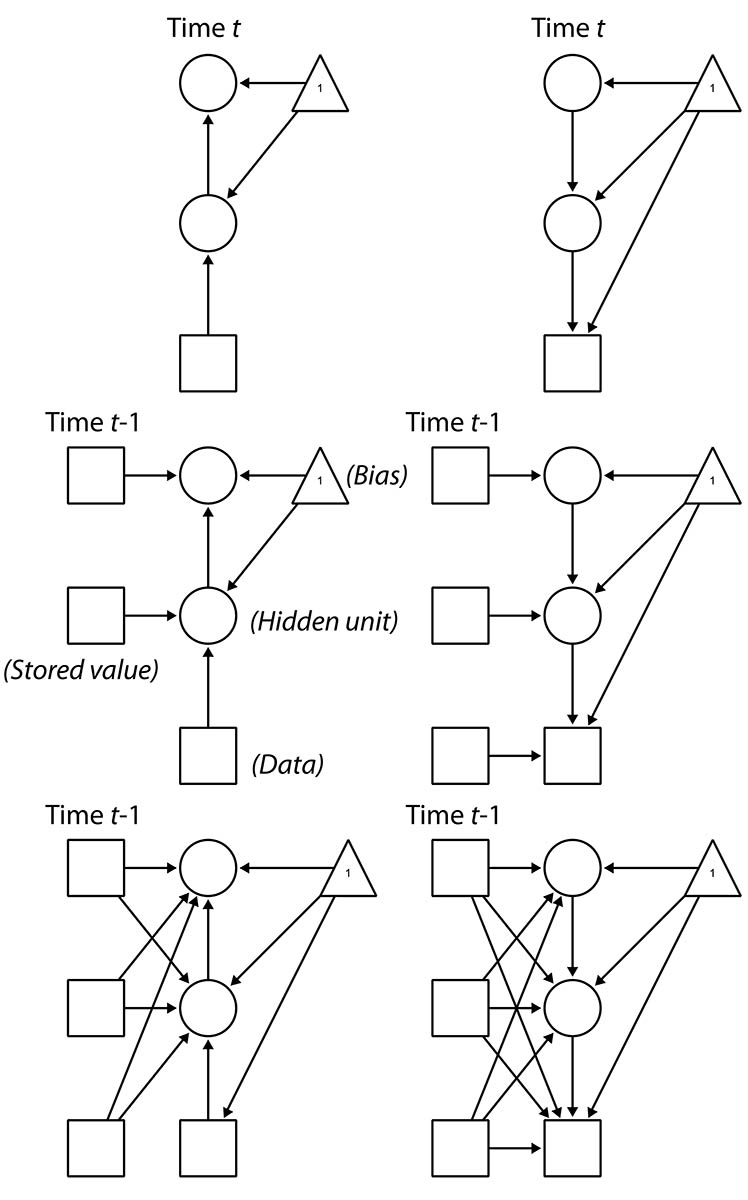
The center row figures show the addition of recurrent elements by storing the last set of hidden node values as fixed. Notice that not only are they fixed, but they are not generated in the sleep phase of learning. Because of this, we can also go on to specify the model in the third row, where all current layers draw from all stored lags. The effect is something akin to both lateral connectivity within-layer and connections that can skip layers.
One unexplored thought is that of un-fixed lagged values of the hidden nodes in the generative (i.e., sleep) phase. What would it mean for learning and recall if the model can “dream” retroactively? Memories in the human brain are not necessarily fixed. Every new recollection of a memory alters it slightly and some memories can be highly distorted by suggestion. In dreams, it’s common to experience a sense of continuity from before the moment of experience or even exact false memories that rationalize what is happening in the dream. I suppose a sensible configuration to try would be to fix the stored values of the observed data but allow past values of hidden nodes at higher layers to be re-evaluated with the addition of new information.
For now, I’ll keep it as simple as possible and let all lagged values remain fixed.
To get started, I changed the list L to have another level of depth, allowing time lags, as hinted by the additional subscript on the variable names _l0…_l3:
For 2 hidden layers of dimension 8 and 4, each with 3 lags, we get:
[[1]]
[1] "bias"
[[2]]
[[2]][[1]]
[1] "x1_l0" "x2_l0" "x3_l0" "x4_l0" "x5_l0" "x6_l0" "x7_l0" "x8_l0" "x9_l0" "x10_l0" "x11_l0" "x12_l0"
[[2]][[2]]
[1] "x1_l1" "x2_l1" "x3_l1" "x4_l1" "x5_l1" "x6_l1" "x7_l1" "x8_l1" "x9_l1" "x10_l1" "x11_l1" "x12_l1"
[[2]][[3]]
[1] "x1_l2" "x2_l2" "x3_l2" "x4_l2" "x5_l2" "x6_l2" "x7_l2" "x8_l2" "x9_l2" "x10_l2" "x11_l2" "x12_l2"
[[2]][[4]]
[1] "x1_l3" "x2_l3" "x3_l3" "x4_l3" "x5_l3" "x6_l3" "x7_l3" "x8_l3" "x9_l3" "x10_l3" "x11_l3" "x12_l3"
[[3]]
[[3]][[1]]
[1] "h1_n1_l0" "h1_n2_l0" "h1_n3_l0" "h1_n4_l0" "h1_n5_l0" "h1_n6_l0" "h1_n7_l0" "h1_n8_l0"
[[3]][[2]]
[1] "h1_n1_l1" "h1_n2_l1" "h1_n3_l1" "h1_n4_l1" "h1_n5_l1" "h1_n6_l1" "h1_n7_l1" "h1_n8_l1"
[[3]][[3]]
[1] "h1_n1_l2" "h1_n2_l2" "h1_n3_l2" "h1_n4_l2" "h1_n5_l2" "h1_n6_l2" "h1_n7_l2" "h1_n8_l2"
[[3]][[4]]
[1] "h1_n1_l3" "h1_n2_l3" "h1_n3_l3" "h1_n4_l3" "h1_n5_l3" "h1_n6_l3" "h1_n7_l3" "h1_n8_l3"
[[4]]
[[4]][[1]]
[1] "h2_n1_l0" "h2_n2_l0" "h2_n3_l0" "h2_n4_l0"
[[4]][[2]]
[1] "h2_n1_l1" "h2_n2_l1" "h2_n3_l1" "h2_n4_l1"
[[4]][[3]]
[1] "h2_n1_l2" "h2_n2_l2" "h2_n3_l2" "h2_n4_l2"
[[4]][[4]]
[1] "h2_n1_l3" "h2_n2_l3" "h2_n3_l3" "h2_n4_l3"
The generative and recognition adjacency weight matrices Wg and Wr now include columns and rows for all of the above labels, so the dimensionality grows quite quickly.
This is where R’s slowness makes it difficult to really evaluate this model.
My work is ahead of me to implement it in Python.
Anyways, the wake-sleep cycle is mostly the same. The bottom-up and top-down expectations have many more terms from the lagged values, but my single-matrix approach easily generalizes to allow for that. There is however extra code appending the matrix of complete node values to store those generated at each iteration in the previous row:
if(t>1) for(l in 1:min(t-1,lags) ) X[t,unlist(lapply(L[-1],"[",l+1))]<-X[t-l,unlist(lapply(L[-1],"[",1))]
This is added to the beginning of each loop that calculates the layer expectations.
#Start values
Wg[Wg.f]<-rnorm(sum(Wg.f))
Wr[Wr.f]<-rnorm(sum(Wr.f))
Wr[Wr==1]<-0
Wg[Wg==1]<-0
nIter<- 500000
for(i in 1:nIter){
# X.gen<-rRHH(n+1, sim.Wg)[-1,]
# dat<-X.gen[,unlist(L[[2]][[1]])]
dat.chunk.seg<-sample(1:(nrow(dat.bit)-chunkSize), size=1 )
dat.chunk<-dat.bit[dat.chunk.seg:(dat.chunk.seg+chunkSize-1),]
n<-chunkSize
X<-matrix(0, n, dim.total, dimnames=list(NULL, dim.v))
X[,1]<-1
X[,unlist(L[[2]][[1]]) ]<-as.matrix(dat.chunk)
#WAKE
for(t in 1:n){
if(t>1) for(l in 1:min(t-1,lags) ) X[t,unlist(lapply(L[-1],"[",l+1))]<-X[t-l,unlist(lapply(L[-1],"[",1))]
x<-as.matrix(X[t,])
for(h in 3:Q){
x[L[[h]][[1]],]<-lgt(Wr%*%x)[L[[h]][[1]],]
x[L[[h]][[1]],]<-rbinom(length(x[L[[h]][[1]]]), 1, x[L[[h]][[1]],] )
}
X[t,unlist(lapply(L,"[",1))]<-t(x[unlist(lapply(L,"[",1)),])
}
X.p<-lgt(X%*%t(Wg))
X.p[,1]<-1
Wg.gr<-t((t(X)%*%(X-X.p))/nrow(X))
Wg[Wg.f]<- (Wg + lr*Wg.gr)[Wg.f]
#SLEEP
X<-matrix(0, n, dim.total, dimnames=list(NULL, dim.v))
X[,1]<-1
for(t in 1:n){
if(t>1) for(l in 1:min(t-1,lags) ) X[t,unlist(lapply(L[-1],"[",l+1))]<-X[t-l,unlist(lapply(L[-1],"[",1))]
x<-as.matrix(X[t,])
for(h in Q:2){
x[L[[h]][[1]],]<-lgt(Wg%*%x)[L[[h]][[1]],]
x[L[[h]][[1]],]<-rbinom(length(x[L[[h]][[1]]]), 1, x[L[[h]][[1]],] )
}
X[t,unlist(lapply(L,"[",1))]<-t(x[unlist(lapply(L,"[",1)),])
}
X.p<-lgt(X%*%t(Wr))
X.p[,1]<-1
Wr.gr<-t((t(X)%*%(X-X.p))/nrow(X))
Wr[Wr.f]<-(Wr + lr*Wr.gr)[Wr.f]
if(i%%5==0) cat("\r",i,"\t\t")
#Output
if(i%%150==0){
cat("\nData:\t")
print(printData(dat.chunk))
cat("\nSleep output:\t")
print(printData(X[,L[[2]][[1]]]))
cat("\nSimulation:\t")
print(printData(rRHH(20, Wg)[,L[[2]][[1]]]))
cat("\n\n")
}
}
I am training this model on the Wikipedia page for the American civil war. I mapped every word to a binary vector, so it can just learn successions of them:
dat<-read.csv("textData.csv", sep=" ", header=FALSE)[,1]
p<-ceiling(log2(length(unique(dat))))
bitMap<-expand.grid(rep( list(0:1), p))[1:length(unique(dat)),]
rownames(bitMap)<-sort(unique(dat))
dat.bit<-bitMap[dat,]
Here are some simulations from 209000 iterations of model dimension c(10,8,6,4) with 5 lags.
Simulation: [1] "NA jeb control tired results bay wagner ( the 112 the presidency newly enthusiasm towards the ferocious forage flotilla dramatically"
Simulation: [1] "miles off the don absolutely violent outgoing emerged were heartland north towards the 260 cover rich NA absolutely overthrow 's"
Simulation: [1] "stationing menace destination 280 the aged religious NA NA that work otherwise militia nullify divisions produced . legal wise .["
Simulation: [1] "homestead 15 use the comprised motivation admission were the single rank the norfolk ) fence enforcement converting the whether were"
Results so far suggest that either this is not a very effective approach to modeling language, or that the complexity is much greater than I can compute in R. I sorted the text-to-binary key in alphabetical order, so you get a lot of alternation between alphabetically adjacent words with random error. Perhaps a non-stochastic network is more sensible.